Zero Knowledge Authentication
A blog post by Blake De Garza, CODEX Engineer
Abstract
Authentication is an important element of the services we interact with on a day-to-day basis. One current methodology of authenticating begins with sending the hash of a username and password—in some instances just the hash of the password [1] and the plain text of the username. This methodology leaves the possibility of replay attacks [1] to gain entry into one of these services, or an insider threat of an administrator having access to viewing, retrieving, and storing passwords inside a database [1]. Almost all the vulnerabilities given by Tsai, Lee, and Hwang [1]: forgery attacks, forward secrecy, mutual authentication, parallel session attacks, and password guessing attacks, can be mitigated by The Zero Knowledge Authentication with Zero Knowledge Protocol [2], which protects against these attack vectors.
Background
Zero-knowledge proofs were first introduced in 1988 by Simmons and Purdry [3] and by Goldwasser, Micali, and Rackoff in 1989 [4]. These papers explore the rigorous mathematical proof of what a zero knowledge and interactive proof system entail [4] while exposing an application toward public key infrastructure (PKI) [3]. Simmons and Purdy [3] provide an introduction into zero knowledge authentication (ZKA), a candidate of design as well as the implementation, and I will examine the attack surfaces to prove ZKA is safer than using a conventional [1] sole-source hash-based authentication mechanism.
ZKA proves a user has entered the correct password client side without actually sending the password information via plaintext or hashtext to the server. At first, zero knowledge might seem counterintuitive—how is the server going to authenticate if it doesn’t have anything to authenticate against? The answer is complex but can be explained through exponential mathematics.
ZKA with zero knowledge (ZKA_wzk) [2] defines the algorithm that needs to take place while mathematically proving it is indeed zero knowledge.
ZKA_wzk Algorithm
Initialization
Given a cyclic group G, let g0 and g2 be random elements of G and the public key is {G, g0}. In other words, g0 is a prime number in the cyclic set of G.
Registration
-
The user inputs a username and password.
-
The client hashes the password using the sha256 algorithm, x = sha256 (password).
-
The client computes a pseudonym for the user Y = g0^x, where x is the hash of the user registration password (initial setup).
-
The client sends (username, Y) to the server so a dictionary can be made and dictionary[‘username’] == Y, for reference later by the server. In this step, only an obfuscation of the password is sent—never the real and actual password. Here all an attacker would gain from snooping is seeing the plain text of a username.
Authentication
-
The client sends an authentication request.
-
The server sends back a one-time token α.
-
The user inputs a username and password (hopefully, the correct combination).
-
The client calculates x2, x2 = sha256 (password), where x2 is the hash of the user-provided password on the client side.
-
The client calculates the user pseudonym Y = g0^x2.
-
The client generates a random number r.
-
The client calculates T1 = g0^r.
-
The client calculates c = sha256 (Y, T1, α), and calculates zx = r–c*x2. Note: zx is different from the variable x.
-
The user sends (c, zx, and the entered username) to the server. At this point, no passwords are sent via plain text.
-
The server fetches Y from the given username.
-
The server calculates T1 = (Y^c) * (g0^zx).
-
The server then verifies c == H(Y,T1,α), where H is a hashing function.
Breaking This Down
T1Client = g0^r and T1Server = (Y^c) * (g0^zx).
Therefore, for authentication to occur,
H (Y_entered,T1_Client, α) needs to equal H (Y_stored,T2_Server, α).
This can only occur if and only if the correct username and password are entered during authentication.
T1client and T1server must be equivalent.
Proof
-
T1_client = g0^r
-
T1_server = (Y_stored^c) * (g0^zx)
-
c = sha256 (Y_entered, T1, α), and calculates zx = r–c*x2
-
Substituting for zx and knowing Y_stored = g0^x
-
T1_server = g0^(cx1)*(g0^[r-cx2])
-
In the instance, x2 == x1 (the password was entered correctly), the correct session token is used and the correct username is entered.
-
T1_server = g0^(cx1 +r–cx2) = g0^(cx1+r–cx1) = g0^(r)=T1_client
Applying the ZKA Algorithm
Figure 1 shows the three Python classes, ZeroAuthClient, ZeroAuthServer, and ExponMath, that were created and how they are implemented in Python from [2].
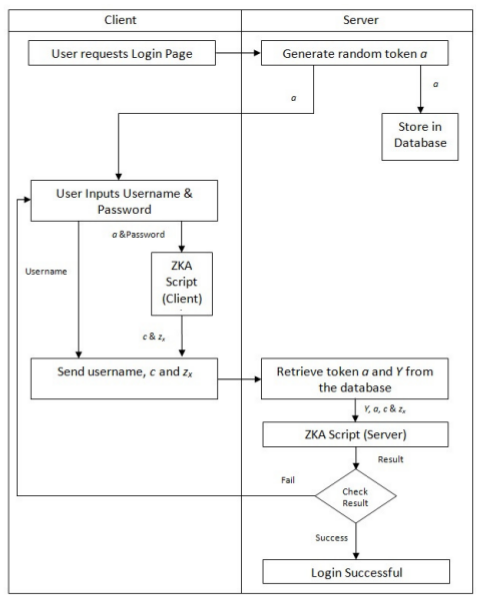
Figure 2. Taken from [2], in this overall algorithm for ZKA, time 0 is at the top and time moves downward
class ZeroKnowledgeAuthClient:
p = int(‘ONE_TIME_PRIVATE_KEY’)
def __init__(self, username, x, randomToken):
G = “12345...cyclic...group...54321”
self.gknot = 3
self.x = sha256(“a_very_secure_password_:_123!”)
self.y = modexp(gknot, int.from\_bytes(self.x, byteorder=’little’),
self.p)
self.r = int(secrets.choice(G))
self.T1 = modexp(gknot, self.r, self.p)
self.a = randomToken
self.c = self.CalculateC()
self.zx = self.r – (self.c *(int.from_bytes(self.x, ‘little’)))
def CalculateC(self):
self.c = int.from\_bytes(Sha256(str(self.Y).encode() +
str(self.T1).encode() + str(self.a).encode()), byteorder=’little’)
class ZeroKnowledgeAuthServer:
p = int(‘ONE_TIME_PRIVATE_KEY’)
def __init__(self):
self.session = self.GenerateSession()
self.gknot = 3 # prime number
def __GenerateSession(self):
self.session = secrets.randbelow(self.p)
return self.session
def Authenticate(self, username, c, z):
self.a = self.session
self.c = c
self.z = z
self.u = username
self.Y = self.LookupPublicKey(self.u)
t1 = natural_modexp((natural_modexp(self.Y, self.c, self.p) *
natural_modexp(gknot, self.z, self.p)), 1, self.p)
digest = int.from_bytes(Sha256(str(self.Y.encode() + str(t1.encode() +
str(self.a).encode()), byteorder=’little’)
if c == digest:
return True # we are successfully Authenticated
else:
return False # we failed to Authenticate
def natural_mod(a, m):
“”” mod returning natural number using identity of b^e == (b^-1)^e mod m
and identity of -a mod m = m -a mod m
”””
invert = False
if m < 0:
invert = True
m = -m
am = a % m
if am < 0:
am += m
assert am >=0 and m >= 0
if invert:
assert am <= m
am = m – am
return am
Discussion
ZKA_wzk stops most of the attack vectors from occurring because the password is never transferred via plain text; the information is in the form of an exponential hash, which makes it obfuscated; and the logarithm of a very large number would then lead to the sha256 of the password. Therefore, log (base g0)[g0^(256bits of freedom)] = sha256 (x) can be found if the server is broken into. However, because sha256 is a one-way hash function, the only way to find x would be through a dictionary attack/rainbow table to find the hash collision. Is this possible? Sure, but this would require connecting and downloading the entire database of user pseudonyms.
ZKA_wzk stops the insider threat from occurring because administrators would not have access to the plain-text passwords and therefore could not ever know the password to other user accounts. The exception, of course, happens if this method is used when an administrator has a rainbow table that finds collisions (unlikely but nonetheless possible).
Using the random session token, ZKA_wzk eliminates replay attacks, which grab the credentials that were sent previously and use them in the future. But because each login requires a new session and the session token is obfuscated within the variable c, it is nearly impossible to replay a session attack, unless the server is, in fact, malicious.
And what about mutual authentication, which guarantees neither the client nor the server are malicious [1]? ZKA_wzk does not provide this mutual authentication alone. For a malicious server to pose as a good server, it must do the following:
1) Calculate the correct variables (needing the session, username, and password at a minimum). Even if the server just sends c, zx, and username, the user has already connected to the correct server, gaining the random session token correctly.
2) The client sends back to this malicious server.
3) The server would then relay those credentials (c, username, and zx) to the original server.
Because this relay could be a lengthy amount of time, the user’s packet could go to the good server before the malicious server. If this happens, the user remains logged in, and the good server knows there is a replay attack occurring.
To ensure mutual authentication, the good server would need to receive the authentication request via asymmetric encryption with the public key of the good server. Therefore, an additional step in the original protocol would need to be added. The token request needs to be sending the user’s session_request + user public key. Then the user decrypts the session key when received from the good server.
Now when the malicious server snatches the credentials, it cannot send those credentials to the original (good) server because the session key, without the private key of the server, will be invalid. Adding the challenge response mechanism to the authentication makes it difficult to reproduce, and the mutual authentication will be correct because both parties have to verify a random number known as a token.
Conclusion
ZKA with zero knowledge is a hardened authentication mechanism because plain text passwords are never stored or shared over the wire. And a mathematical proof known as verifier (client) and a prover (server) must be there to gain access to the encrypted data. However, ZKA does not ensure mutual authentication unless there is a challenge response built in, i.e., the session token is shared through asymmetric cryptography.
Alas, as in life, nothing is perfect and there are theoretical attacks against this approach, even if the attacks are man in the middle and not snooping attacks. Either way, ZKA with zero knowledge is still more secure than the modern authentication mechanisms shared in [1] because the protocol proves the correct password was in fact entered without ever directly sharing the user’s password.
Bibliography
[1] Tsai, C.-S., C.-C. Lee, and M.-S. Hwang. 2006. Password authentication schemes: Current status and key issues. International Journal of Network Security, 3(2), 101–115.
[2] Lum Jia Jun, Brandon. 2010. Implementing Zero-Knowledge Authentication with Zero Knowledge (ZKA_wzk). The Python Papers Monograph 2:9, Proceedings of PyCon Asia-Pacific, 2010.
[3] Simmons, G. J., and G. B. Purdy. 1988. Zero-Knowledge Proofs of Identity and Veracity of Transaction Receipts. In: Barstow D. et al. (eds) Advances in Cryptology—EuroCrypt’88. Lecture Notes in Computer Science, vol 330. Springer, Berlin, Heidelberg.
[4] Goldwasser, S., S. Micali, and C. Rackoff. 1989. The Knowledge Complexity of Interactive Proof Systems. Society for Industrial and Applied Mathematics, 18(1), 186–208, February 1989.